Bitwise Operators

Learning Objectives

• Be able to isolate a bit or a group of bits using C++.
• Understand bitwise AND, OR, and NOT (inversion).
• Differentiate between an inclusive OR and an exclusive OR.
• Differentiate between a left shift and a right shift.
• Differentiate between an arithmetic right shift and logical right shift.
• Understand how negative numbers are identified in computers.
• Understand how left shift and right shift can perform quick multiplication and division of powers of two.
• Be able to test one or a set of bits in any data type.
• Be able to set one or a set of bits in any data type.
• Be able to clear one or a set of bits in any data type.

---

The smallest addressable memory unit in our modern computers (Intel/AMD, ARM, RISC-V, MIPS) is one byte. However, that's 8-bits! So, what do we do to get to the bit level? We sort of have to fake it by "shifting" bits around. The term bitwise means "at the bit level". So, a bitwise AND is an AND operator that operates on individual bits.

We have seen the logical comparison operators, such as && and ||, and how they work. Recall that a && b must have both a and b be true for the entire expression to be true. We are going to use the same logic, except now we do it for each bit in a number.

---

AND, OR, and NOT Bitwise Operators

Bitwise operators operate on individual binary digits. When you add two numbers, you line all of the digits places in columns. The same happens here. Each place (ones, twos, fours) of one number gets placed on another.

AND

The AND operation is a binary operator, meaning that it takes two operands (much like add, subtract, multiply, and divide). When we line all of the digits places, if there are two 1s, the result is a 1. Any other case, the output is a 0. The following table shows the inputs and outputs of the AND operation.

Top operand	Bottom Operand	Output
0	0	0
0	1	0
1	0	0
1	1	1

As you can see here, when we stack the bits and align them in the correct digits order, the only way we can get an output of 1 is for both the top and bottom to be 1. Any other case will result in a 0 for that digits place.

In C++, the AND operator is specified by an ampersand (&), and is demonstrated as follows.

int a = 7;
int b = 6;
int c = a & b;
printf("%d", c);

To manually determine what C++ is going to print out above, let's follow the checklist below:

1. Convert all numbers to base 2 (binary).
2. Align each digits place of one number over those of the other (digit places must be in the same column).
3. Perform operation.
4. Convert to whatever base is necessary.

Let's take step 1 and convert 7 and 6 into binary. \(7_{10}=0111_{2}\) and \(6_{10}=0110_2\). Now, let's line them up:

  0111  <--- int a  (7)
& 0110  <--- int b  (6)
-------
  0110  <--- result (6)

Since we're working in base 2, you can see that this is in fact bitwise. In the actual computer, there will be 32 digits since an integer is 32 bits.

The AND operator is commutative meaning that a&b is the same operation as b&a.

Inclusive OR

An inclusive OR is usually shortened to just OR whereas exclusive or is shortened to XOR (ex-OR). Just like the AND operation, this is performed bitwise after we align each digit place in the same column.

Top operand	Bottom Operand	Output
0	0	0
0	1	1
1	0	1
1	1	1

Unlike an AND, as long as there is a 1 ANYWHERE in the column, the result for that digit place is a 1.

int a = 8;
int b = 6;
int c = 8 | 6;
printf("%d", c);

1. Convert all numbers to base 2 (binary).
2. Align each digits place of one number over those of the other (digit places must be in the same column).
3. Perform operation.
4. Convert to whatever base is necessary.

  1000  <--- int a  (8)
| 0110  <--- int b  (6)
-------
  1110  <--- result (14)

Notice that in each column, as long as a 1 is present, the result for that place is also a 1.

Just like AND, inclusive OR is also commutative.

Exclusive OR (XOR)

The exclusive OR (XOR) operator is much like the OR operator except that EXACTLY one 1 must be present in each column. Let's take a look at the truth table for XOR.

Top operand	Bottom Operand	Output
0	0	0
0	1	1
1	0	1
1	1	0

1. Convert all numbers to base 2 (binary).
2. Align each digits place of one number over those of the other (digit places must be in the same column).
3. Perform operation.
4. Convert to whatever base is necessary.

int a = 7;
int b = 6;
int c = 7 ^ 6;
print("%d", c);

  0111  <--- int a  (7)
^ 0110  <--- int b  (6)
-------
  0001  <--- result (1)

As you can tell, if there are two zeros or two ones, the result is a zero, otherwise it is a one.

NOT (invert)

The NOT is also called the one's-complement. All we do is look at all of the bits and flip all 0s to 1s and all 1s to 0s--essentially inverting all of the bits. This is a unary operator since it only operates on one operand.

char a = 7;
char b = ~a;
printf("%d", b);

~0000 0111  <--- char a (7)
----------
 1111 1000  <--- result (-8)

You might be asking yourself, "how does that become -8?" This will be explained below. However, the most important part of the NOT operator is that you need to pad it out to the data size. A char is 8-bits, so I am required to write out all 8 bits since EVERY digit is going to be flipped. If this was a short, I would need 16 digits, an int would need 32 digits, and a long would need 64 digits (except for some Windows machines).

---

Binary Signs (Negative/Positive)

A computer stores 0s and 1s usually for off and on, respectively. However, what does a computer have to do to store a negative number? There is no dash (-) or plus (+) in binary. Instead, a computer uses the most-significant bit as the sign bit. The most significant bit is the leftmost digit. This is why you must know the data size before determining if it is a negative number.

Let's look back at what I produced using ~7, which was -8: 0b1111_1000. We look at the leftmost bit. If this bit is a 1, the number is negative, if it is a 0, the number is positive. The tricky part is that negative numbers are stored in two's-complement format. Therefore, if we see that the sign bit is a 1, we can't just get rid of it and figure out the magnitude of the operand.

Recall that one's complement was simply flipping all bits (0s to 1s and 1s to 0s). The two's complement is as simple. We perform the one's complement then add 1. That's it! So, let's check our number: 0b1111_1000. We know it's negative (if it is a char) because the 8th bit (digit place \(2^7\)) is a 1. Now, let's flip all the bits and add 1 to see what its positive value is: ~0b1111_1000 = 0b0000_0111. Then, we add 1 = 0b0000_0111 + 1 = 0b0000_1000. This is the value 8. Since we know the value is negative, the final result is -8.

1. Check most-significant bit (leftmost bit) of a signed data type.
   1. If the bit is 0, the value is positive. Read the value as written.
   2. If the bit is 1, the value is negative. Perform two's complement to get the positive value. Attach a negative sign to it and you have your magnitude.

---

Bit Shifting

There are three ways we can shift bits: logical left shift, logical right shift, and arithmetic right shift. A shift essentially means to shift all of the bits together left or right. Each shifting operation takes a value and the number of places to shift. In C++, we use << for left shift and >> for right shift. C++ will distinguish between an arithmetic right shift and logical right shift based on the data type. Unsigned data types always use logical right shifts whereas signed data types always use arithmetic right shifts.

A shift just moves each digit right by a certain number of places or left by a certain number of places. Since we only have a certain number of digits, those bits that "fall off" the left or "fall off" the right are discarded.

int value_left = 71 << 1;   // Take 71 and shift all bits left by 1
int value_right = 71 >> 1;  // Take 71 and shift all bits right by 1

71 is the value 0b100_0111. However, for this, we have to know when we drop digits. 71 is an integer literal, meaning that it is a 32-bit, signed value. So, let's expand this value: 0b0000_0000_0000_0000_0000_0000_0100_0111. Now, when we shift all digits left one place, we get: 0b0000_0000_0000_0000_0000_0000_1000_1110. Notice that when the one's place moved to the two's place, a zero replaced the ones place.

Left Shift

Let's demonstrate an example here. Let's take the value 9 (binary 1001) and shift it left 4 places to see what we get. First, we need to know our data size, so in C++, 9, would be an integer literal, which is 32-bits:

int result = 9 << 4;
printf("%d", result);

As you can see, all of the bits are shifted to the left by four places. The upper four digits (which were all zeroes) are discarded (represented by red in the figure above). The lower four places (1001) were moved and in their original spot, 0s were replaced (represented in green in the figure above).

Right Shift

Recall that there are two right shifts: arithmetic and logical. A logical right shift mimics the left shift except we move right instead of left. Values fall off the right and values on the left are replaced with zeroes. An arithmetic right shift does the exact same thing except instead of replacing zeroes on the left, it duplicates the sign bit.

Using Shifts for Quick Math

Right shifts shift all bits to the right by a provided number of places in binary. If we did this in decimal, we can see that we divide by 10 each place we move right: \(1000 >> 1=100=\frac{1000}{10}\). So, we can say a right shift is \(\frac{a}{10^x}\). Where a is the original value and x is the number of places we shift right.

With bitwise operators, we're shifting bits, so it's base 2. However, the formula is the same. \(0100_2>>1=0010_2=\frac{0100}{2}\). When we shift 4 >> 1, we get the value 2. So, the same formula holds: \(\frac{a}{2^x}\), where a is the original value and x is the number of places we shift right.

This should start cluing you into why we have two right shifts. Let's take -4 as an 8-bit value: \(1111\_1100_2\). If we do a right shift, we'd expect -2 (\(\frac{-4}{2^1}\)). However, if we did a logical right shift, we would get \(1111\_1100_2>>1=0111\_1110_2=126_{10}\). How did we go from -4 to 126? That's because a logical right shift destroys the sign bit.

An arithmetic right shift fixes this by replacing empty digits with the sign bit instead of 0s. So, given our example above, we would do: \(1111\_1100_2>>1=1111\_1110_2=-2_{10}\). That's better! Notice a 1 replaces the sign bit instead of a 0. This yields us a -2, which is exactly what we wanted.

There is only one left shift, the logical left shift. Unlike right shift, a left shift multiplies the value by 2 for each shift. The formula is \(a << x=a\times 2^x\) where a is the original value and x is the number of places you left shift. Obviously, there is a limit since we do not have infinite digits.

Once again, an arithmetic right shift is used by C++ whenever the data type is signed and a logical right shift whenever the data type is unsigned. In C++, all integral data types are signed by default. You can use the unsigned keyword in C++ to remove the sign bit; however, you can no longer store negative numbers.

int a = 100;        // implicitly signed integer
signed int b = 100; // explicitly signed integer
unsigned int a = 100; // explicitly unsigned integer

Unsigned Data Types

A char stores 8-bits, but one bit is used to store the sign. Therefore, only 7 bits are available to store the number's magnitude. \(2^7=\pm~128\). Due to two's complement, we actually have a range of -128 to 127: \(\text{~}1000\_0000_2+1=0111\_1111_2+1=1000\_0000_2=-128\) and \(0111\_1111_2=64+32+16+8+4+2+1=127\).

Type	Size (bytes)	Signed Range	Unsigned Range
char	1	-128 to +127	0 to 255
short	2	-32,768 to +32,767	0 to 65,535
int	4	-2,147,483,648 to +2,147,483,647	0 to 4,294,967,295
long	8 (4 on Windows)	-BIG to +BIG	0 to BIG

Note about Windows: If you use Visual Studio or any of the Microsoft developer tools, a long data type is only 4 bytes. You must use long long. On Linux (your lab machines and Mac) a long is 8 bytes.

Notice that with unsigned, we lose the ability to store negative numbers, but we double the capacity. This is because we don't waste a bit storing the sign. Recall that a char is 8 bits. If we take the sign bit off, then we have all 8 bits to store data: \(1111\_1111_2=128+64+32+16+8+4+2+1=255\). Finally, ONLY integral data types can be unsigned. There is NO such thing as an unsigned float or unsigned double.

This is why C++'s vector.size() member function returns an unsigned int. It's not possible to have a negative size, but we can double its effective range by using an unsigned int.

Uses

So what's this all about? Who cares about getting to the bit level? Usually hardware developers do. A register is a piece of memory in hardware. We can use a char to control 8 light-emitting diodes (LEDs). If I set a 1 in one the bits, it illuminates that LED. If we didn't have bitwise operators, we'd need 8-bits for each LED!

Test

If we want to test a certain bit, we create what is called a mask. This is a group of bits that blocks all bits but the ones we're looking at. We typically use AND to get certain bits. For example, say we want to see if bit 5 is a 1 or a 0. We would first shift bit 5 into the one's place and AND it with the value 1. Here's why:

char value = 121;
if (1 == ((value >> 5) & 1)) {
     printf("Bit 5 is 1!\n");
}
else {
     printf("Bit 5 is 0!\n");
}

Let's take an 8 bit value 121 which is a signed char: \(121=0111\_1001_2\). From right to left, we start with bit 0 through 7. So, we want bit 5. If we shift 121 right 5 places, we get \(0000\_0011_2\). This is the value 3, so we didn't isolate a single bit (which is either 1 or 0). However, if we AND this with 1, it will give us ONLY the 1s place, which is 1. This is called testing a bit.

  0000 0011  <-- original value
& 0000 0001  <-- mask
  ---------
  0000 0001  <-- one's place is 1

Set

Setting a bit means to set a given digit's place to the value 1. If it is already 1, it resets that 1 back to 1, essentially doing nothing. All other bits are left alone. Our goal is to shift a 1 over to the place we need it and OR it with the original value. Everything else is 0, recall that \( x | 0 = x\) meaning anything OR'd with 0 is itself, this allows us to ONLY change the bits we want. Say we want to set bit 5.

char value = 8;
value |= (1 << 5); // set bit index 5 (two's place)

  0000 1000   <--- value (8)
| 0010 0000   <--- 1 << 5 (32)
  ---------
  0010 1000   <--- result (40)

Notice that the every place was left untouched except the bit we wanted to set. When we make a bit the value 1, it is called setting the bit.

Clear

Clearing a bit means to set that digit's place to 0 (the opposite of set). In this case, we need to do the same thing we did with set. However, recall that if we OR anything with 0, we get the original value, NOT zero. So, we need to use AND. Instead of putting a 1 in the digit's place we want, we need to put a 0. Anything AND'd with 1 is itself, so that allows us to leave the rest of the digits untouched.

char value = 7;
value = value & ~(1 << 2); // Clear bit index 2

In the code above, we clear bit 2. How? Well, when we do 1 << 2, everything is zero except the 4s place (\(2^2=4\)). However, recall that we want everything to be 1 except the place that we want to clear so that we can AND it and clear just that one place. (1 << 2) is the value 0b0000_0100, but the tilde (~) flips all 0s to 1s, which gives us 0b1111_1011.

  0000 0111  <--- value (7)
& 1111 1011  <--- ~(1 << 2)
  ---------
  0000 0011  <--- result (3)
  

Notice that when we AND with 1, that place's value didn't change. We essentially moved a 0 under the place we wanted to clear and AND'd it. Anything AND'd with 0 is 0.

Example

Write a function called write_value() that takes an 8-bit value and puts those 8-bits in a 32-bit register between bits [21:14], do not change any other bits.

First, we have to understand what this question is asking. We have an 8 bit value, but the register we're writing has multiple fields. We can write numerous examples, but the following is a diagram of what we're looking at here.

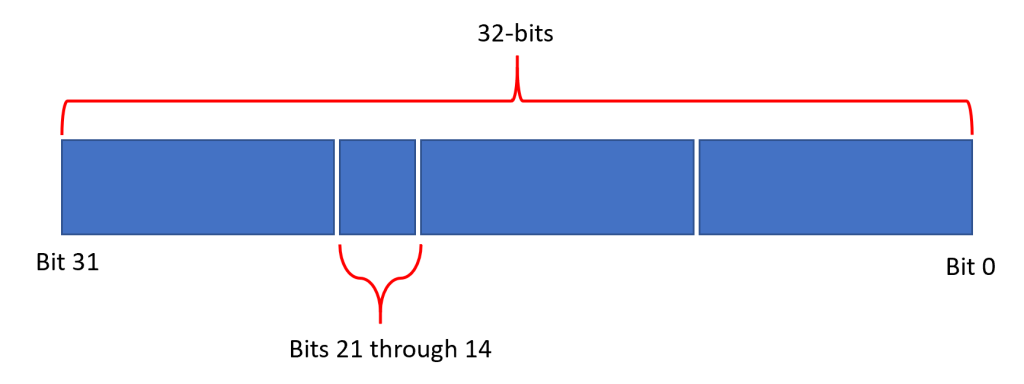
So, essentially, we're given a value to write just in that little slice. Everything else must be left alone. So, let's plan this out. (1) Let's read the current value of the register so that we don't touch the other bits. (2) Let's clear out bits 21 through 14 so that we can use our set function above. (3) Let's shift our 8-bit value left by 14 places to get it in the right place. (4) OR those values together to get the final result. (5) Write the entire 32-bits back into the register.

void write_value(unsigned char value, unsigned int *reg) {
      unsigned int current_reg = *reg;  // read current value
      current_reg &= ~(0xff << 14);  // 0xff is exactly 8 bits
      current_reg |= static_cast<unsigned int>(value) << 14; // write value
      *reg = current_reg;
}

0xff above is called a mask, here's what we're doing with it:

31                                     0
 0000_0000_0000_0000_0000_0000_1111_1111  <-- 0xff
 0000_0000_0011_1111_1100_0000_0000_0000  <-- 0xff << 14
 Bit 21 -----^        ^---- Bit 14

Then we invert it and run the AND operation to clear ALL of those 8 bits out. The reason is because we don't know what's in there. If we OR a 0 there and the original value is 1, the new value is also 1, NOT 0!

So, why the static_cast? Recall that the value is only an 8-bit value. If we shift an 8-bit value left by 14 places, we discard anything that falls off of bit index 7. So, if we static cast this into an integer, we now have 32-bits to play with. When we left shift, those digits won't fall off the left. Be VERY careful about your data types!

Ok fine, but how did you come up with 0xff? Well, we need to inclusively count bits 21 through 14 (21, 20, 19, 18, 17, 16, 15, 14), that's 8 bits. Recall that each hex digit is exactly 4 bits. So, \(\text{f}_{16}=1111_2\). So, we can make an 8-bit mask by putting 0xff together.

---

Video