Learning Objectives
- Be able to add two binary numbers together without converting bases.
- Be able to subtract two binary numbers without converting bases.
- Be able to multiply two binary numbers without converting bases.
- Understand size constraints when multiplying two numbers.
- Be able to divide two binary numbers without converting bases using the restoring division algorithm.
- Understand what constitutes an overflow and how to detect one.
- Understand what happens when a value is widened or narrowed.
- Differentiate between zero-extension and sign-extension.
Introduction
Essentially, we're going to look at what addition, subtraction, multiplication, and division actually are and how we can do it in base 2. If we follow what we're doing in base 10, we can simply "convert" our thinking to base 2.
Addition
When we add two numbers together, we're combining two "blocks" of values together. This is no different in base 2. The only issue comes from when we carry a value out of a digit's place that can't hold it. For example 9 + 7 is 6 carry the 1 into the 10s place for the final value 16. With base 2, we can easily overflow the next digit (two's place) if we have more than two values being added together.
Let's take just one place and see what we get:
| Top Operand | Bottom Operand | Carry In | Sum | Carry Out |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
In the table above, we can see that \(1_2+1_2=0_2\). This is because 1 + 1 is in fact the value 2, which is \(10_2\), so we "overflow" our digit's place (one's place) and carry out a 1 to the next digit's place, the two's place.
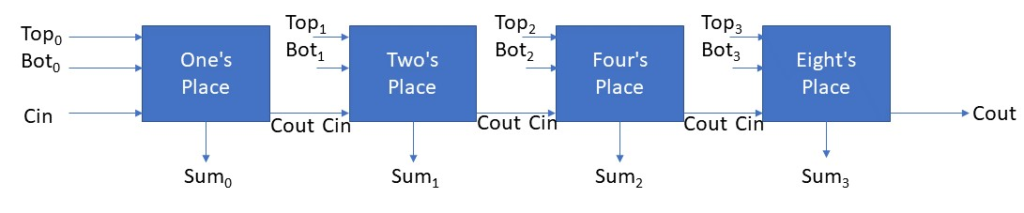
Carry
Notice that the truth table above has a carry out as an output and a carry in as an input. These adders are connected together, and there is one adder per digits place. So, they are connected together. The carry out of the one's place will then be the carry in input to the two's place. The carry out of the two's place will then be the carry in input to the four's place. This goes on and on. For integers, there are 32 of these connected together--one for each bit. For longs, there are 64 of these connected together--again, one for each bit.
Example
Perform \(1011_2 + 0101_2\).
111 <--- carry out 1011 <--- top operand (11) + 0101 <--- bottom operand (5) ----- 10000 <--- result (16)
Overflow
You can see in the example above that we come back with a 5 digit number. For math on paper, this is fine since we have an infinite number of digits. In a computer, we aren't given infinite digits--there are only so many transistors we can fit. If we require more digits than are available, we call this condition an overflow. Sometimes an overflow is good, as you'll see with adding a negative number in two's complement format. Other times, it completely skews our number since we've effectively lost a digit.
Adding Negative Numbers
Recall that negative numbers are stored in two's-complement format, meaning that we flip all of the bits and add 1. One neat detail about two's complement is that we can add normally to it and get the correct result. For example, let's add -7 and 6. We should get -1. Since we're using two's complement we need a data size...remember the most significant bit (leftmost) determines if a number is negative.
$$-7_{10}=\text{~}0000\_0111_2+1=1111\_1001_2$$
AND
$$6_{10}=0000_0110_2$$
1111 1001 <--- top value (-7) + 0000 0110 <--- bottom value (6) --------- 1111 1111 <--- result (-1)
We can see that the result is all 1s using 8 bits. This signifies that this is a negative number. So, let's see its magnitude: \(\text{~}1111\_1111_2+1=0000\_0000+1=1\). So, our answer is -1. -7 + 6 is indeed -1. With the two's complement system, we just need to add normally!
Subtraction
Subtraction is much easier done by just taking the two's complement of the right (or bottom) operand and adding. In fact, most adders are built to do just this. For example, 8 - 4 is identical to 8 + -4. We'll use that to our advantage.
Using binary arithmetic, what is 8 - 4?
1111 <--- carry 0000 1000 <--- 8 + 1111 1100 <--- -4 --------- 0000 0100 <--- 4
With our carry, notice that we keep carrying until we run out of digits. This is one example where we use overflow to our advantage, and it is one reason that two's complement works!
Multiplication
Multiplication follows all of the same rules in binary that it did in decimal. However, it's much simpler because we're only multiplying 1s and 0s--the two easiest numbers to multiply. However, there is a "trick" because we're using 1s and 0s. Much like the trick where if you see trailing zeroes, you can just write those down without having to go through the long-hand math.
Using binary arithmetic, multiply 8 and 4.
0000 1000 <--- 8
x 0000 0100 <--- 4
---------
0000 0000 <--- one's place
00000 0000 <--- two's place (add a 0)
+ 000010 0000 <--- four's place (add two 0s)
-----------
0010 0000 <--- result
Notice that we can think of these as decimal numbers when performing arithmetic on paper. You can see that when we multiply 8 and 4, we get the value 0b10_0000, which is 32. Let's take at an algorithmic version of this. Since we're dealing with just 0s and 1s, we're making a decision to add the multiplicand or not. The multiplier makes the decision. If there is a 1 in the digit's place that we're looking at, we add the multiplicand. If there's a 0, we skip and move on to the next digit's place.
Take a look at each one of the three results we get for the example above. If we perform a left shift on the top number, we go from 1000 to 10000 to 10000. Notice this is a way where we can add a zero to the right of the number.
So, when do we stop? Well, we will keep adding the top number as long as there is a 1 in the digit's place we're looking at (starting at the one's, moving to the two's, the four's, and so on). So, whenever the bottom number only contains zeroes, we no longer have to keep adding the top number. This will be your condition to end multiplying.
Notice that when we multiply, we may well exceed the size of our original data size. In most systems, we require two-times the size of the original. In Intel/AMD, after multiplication, two registers were used to hold the product. With 64-bit systems, we don't worry as much because 64-bits can hold a lot of information. However, if you don't take care with your data sizes, multiplication can easily lead to overflows.
In multiplication, we generally only multiply positive numbers. This means we only need one multiplication function for both signed and unsigned numbers. Before we send our multiplier and multiplicand to that function, however, we need to check the most significant bit. If it's 1, we take the two's-complement and remember that we saw a negative number. Recall that in arithmetic, if we multiply a negative with a positive, we get a negative result. In essence, if we multiply like signs, we get a positive product, otherwise we get a negative product.
bool multiplier_negative = ((multiplier >> 31) & 1) == 1;
bool multiplicand_negative = ((multiplicand >> 31) & 1) == 1;
bool result_negative = false;
if (multiplier_negative) {
multiplier = twos_complement(multiplier);
result_negative = !result_negative;
}
if (multiplicand_negative) {
multiplicand = twos_complement(multiplicand);
result_negative = !result_negative;
}
int product = multiply(multiplier, multiplicand);
if (result_negative) {
product = twos_complement(product);
}
return product;
The code above checks the sign bit of a 32-bit multiplier and multiplicand to see if they're negative. Then, we take the two's-complement of any negative values. We could easily use the - (negation) operator, but I want to show what's happening here. We run our now positive values through the multiply function to get a product. Before we're done, we need to see if our product needs to be negative based on the two operands.
Division
There are several division algorithms, including restoring division, non-restoring division, and repeated subtraction. We will be discussing the easiest, which is the repeated subtraction algorithm. Essentially, we keep subtracting the divisor from the dividend. Whatever is left when the dividend < divisor is called the remainder. The number of times we subtracted the divisor from the dividend is the quotient.
Example
Divide 17 by 7.
17 - 7 = 10 - 7 = 3
We were able to subtract 7 twice, and what was left over was 3. So, the quotient is 2 and the remainder is 3.
struct Result {
unsigned int quotient;
unsigned int remainder;
bool divide_by_zero;
};
Result divide(unsigned int dividend, unsigned int divisor) {
if (divisor == 0) { return {0, 0, true}; }
Result result = {0, dividend, false};
while (result.remainder >= divisor) {
result.quotient += 1;
result.remainder -= divisor;
}
return result;
}
Restoring Division
One binary algorithm for dividing two integers is called restoring division. This allows for a quotient and a positive remainder. There are other algorithms that allow for negative remainders, but we're used to positive, so we'll learn the restoring division algorithm.
Just like repeated subtraction, we need to make a test of the operands to see if we are divisible or not. Recall that in long-division we add the next place if the digit's place is not divisible. We do the same with restoring division.
struct Result {
unsigned int quotient;
unsigned int remainder;
bool divide_by_zero;
};
Result restoring_divide(unsigned int dividend, unsigned int divisor) {
if (divisor == 0) { return {0, 0, true}; }
Result result = {0, 0, false};
long Remainder = dividend; // Use capital R to signify its increased capacity
long Divisor = static_cast<long>(divisor) << 32;
// Now, we go bit-by-bit to see what each digit's place gets (a 1 or a 0)
for (int i = 31;i >= 0;i--) {
Remainder = (Remainder << 1) - Divisor;
if (Remainder >= 0) {
result.quotient |= 1 << i; // set bit i
}
else {
Remainder += Divisor; // restore the divisor
}
}
result.remainder = (Remainder >> 32);
return result;
}
The restoring division algorithm is based on the following division recursive formula:
$$R(i+1)-D\times 2^i=R(i)$$
This is why we need an IF statement. The if statement checks this relationship. If we're wrong, then we have to add (restore) the divisor. Otherwise, we set the bit to 1 of that digit's place, and hence mark its (partial) magnitude. You probably recognize the \(2^i\). This is essentially a left shift. This is why we need to store the divisor left shifted by 32 places long D = static_cast<long>(divisor) << 32;, since when we're at digit index 31, \(2^i\) will start at bit index 32. We need to static cast this because an integer shifted left 32 places will overflow and always be zero.
Restoring division is much more efficient than repeated subtraction. In fact, on some tests (that I quickly did on my computer), restoring division is 10 times more efficient.
Data Type Widening and Narrowing
Putting a smaller data type into a larger data type, such as an integer into a long, is called widening. Whereas putting a larger data type into a smaller data type is called narrowing. When we narrow, we just take the least-significant bits. For example, if we narrow an integer into a char, we take the LOWER 8 bits from the integer (indices 0 through 7). This obviously can change the original value considerably. Widening can be done in one of two ways: sign-extension or zero-extension. What this means is that we need to add bits, so how do we do that? A sign extension replicates the sign bit (most significant bit) of the smaller data type into the larger data type. This is the default in C++ for all signed data types. A zero extension just means we add zeroes to pad a smaller number into a larger number. This is the default in C++ for all unsigned data types.
Examples
What is the value of i when the following occurs? int i = static_cast<char>(-8) ?
-8 as a char is 8 bits, which is 0b1111_1000. ALWAYS ignore the left hand sign of the equals sign. It doesn't matter until everything to the right has been completed. So, (char) -8 will narrow -8 (which is an integer literal). Then, when we set it equal to int i, it will widen back to 32 bits. Now, we need to consider if this is going to be a sign-extension or zero-extension. Remember that if we're widening FROM a signed data type, it'll sign extend. Well, by default all integral data types are signed, so we widen -8 using sign extension. We know we need to go from 8 bits to 32 bits and that sign-extension means to duplicate the sign bit.
In this case, the leftmost bit of -8 as a char is 1, so we will replicate 24 1s to widen an 8-bit value to a 32-bit value: \(1111\_1000_2~\rightarrow~1111\_1111\_1111\_1111\_1111\_1111\_1111\_1000_2\). We can take the two's complement to see that this is still the value -8. Negative numbers' values do not change as long as we add 1s in front of them, much like adding 0s in front of a positive number doesn't change its value.
Let's do the same thing, except zero extend it to see what happens. So, we need to change what we're storing into: int i = static_cast<unsigned char>(-8);
In this case, we're widening from an unsigned data type. Remember, it doesn't matter what we're going INTO, just FROM. So, this will cause C++ to zero-extend -8 into 32-bits:
$$-8_{10}=1111\_1000_2\rightarrow 0000\_0000\_0000\_0000\_0000\_0000\_1111\_1000_2$$
If we look after zero extension, we essentially made -8 into 248 (128+64+32+16+8). This is why it is VERY important to know if we're sign extending or zero extending. Luckily, the rules are simple. Notice that even though we're going INTO a signed integer it still zero-extended. It only matters what we're coming FROM. The only change I made between these examples is that I cast -8 as an unsigned char to zero-extend whereas casting -8 as a signed char sign-extends.
When we get into assembly, it is very important to know what the machine is going to do. Some machines default to sign-extending, others default to zero-extending, and some mix both--just to be confusing :).